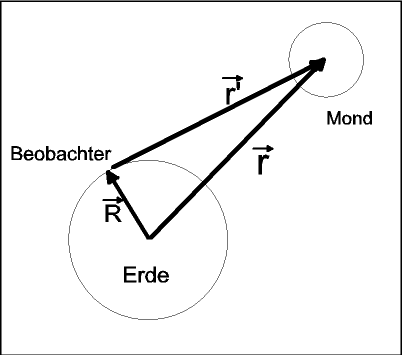
Topozentrische Koordinaten des Mondes
Die Koordinaten Rektaszension, Deklination und Entfernung beziehen sich auf die Mittelpunkte von Erde und Mond, sie werden geozentrische Koordinaten genannt. Für einen Beobachter auf der Erdoberfläche gelten topozentrische Koordinaten.
![]()

Die Beziehungen zwischen geozentrischen und topozentrischen Koordinaten lassen sich anschaulich mit Vektoren darstellen:
![]()
r' ... topozentrische und r ... geozentrische Koordinarten, R ... Ort des Beobachters
Der geozentrische Mondort:
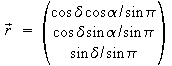
![]() ...
Deklination,
...
Deklination,
![]() ...
Rektaszension und
...
Rektaszension und
![]() ...
Äquatorial-Horizontalparallaxe.
...
Äquatorial-Horizontalparallaxe.
Die Äquatorial-Horizontalparallaxe ist vom Mondmittelpunkt gesehen der Winkel zwischen Erdmittelpunkt und Horizont am Äquator. Die Beziehung zwischen Entfernung und Parallaxe:
![]() (
(![]() in
km)
in
km)
Der Halbmesser des Mondes:
![]()
Der Beobachtungsort:
Er wird für den betreffenden Zeitpunkt wie der Mondort im rotierenden Äquatorsystem angegeben. Dabei wird die geozentrische anstelle der geografischen Breite und die Sternzeit anstelle der geografischen Länge benutzt:
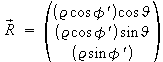
Die Ausdrücke
![]() und
und
![]() werden
nicht aufgelöst und aus den geografischen Koordinaten berechnet,
wobei
werden
nicht aufgelöst und aus den geografischen Koordinaten berechnet,
wobei
![]() der
Abstand des Beobachters vom Erdmittelpunkt in Erdradien ist:
der
Abstand des Beobachters vom Erdmittelpunkt in Erdradien ist:
![]()
![]()
die Hilfsgröße u :
![]()
und das Verhältnis von Pol- und Äquatorradius:![]()
Die lokale Sternzeit![]() des Beobachtungsortes:
des Beobachtungsortes:
![]()
![]() ist
die Sternzeit in Greenwich und
ist
die Sternzeit in Greenwich und
![]() die
geografische Länge (positiv westlich und negativ östlich).
die
geografische Länge (positiv westlich und negativ östlich).
Topozentrische Koordinarten:
Mit Gleichung
![]() sind die topozentrischen Koordinarten
sind die topozentrischen Koordinarten
im rechtwinkligen System: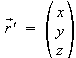
und im Polarsystem:
![]()
![]()
![]()
![]()
Umgekehrt lassen sich aus den topozentrischen auch die geozentrischen Koordinaten berechnen:
![]()
Wofür werden die topozentrischen Koordinaten benötigt?
Konstellationen des Mondes mit Sterne und Planeten
Sternbedeckungen
Sonnenfinsternisse.
Für Sonne und erdnahe Planeten sind ebenfalls topozentrische Koordinarten zu verwenden. Die Berechnung ist einfacher und wird auf einer speziellen Seite dargestellt.
Mit weiteren Überlegungen kann man die vektorielle Darstellung auch auf Erdsatelliten anwenden.
Beispiel:
Topozentrische Koordinaten des Mondes für 2000 November 29, 18.30 MEZ für einen Ort mit den geografischen Koordinarten Länge = -10° und Breite = 52°, Höhe über dem Meeresspiegel = 250 m.
Die geozentrischen Koordinaten des
Mondes:
![]() ,
,
![]() ,
,
![]() ,
entspricht
,
entspricht
![]() .
.
Die Sternzeit:
![]()
![]() (
(![]() in
Grad)
in
Grad)
(u = 51,90660783°)
![]() ,
,
![]()
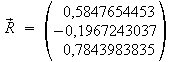 ,
,
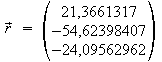 ,
,
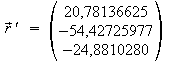
Ergebnisse:
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Karl-Heinz Bücke
02. Oktober 2000